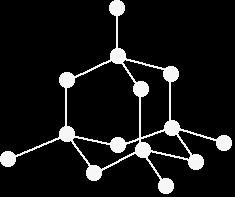
GIANT COVALENT STRUCTURESThis page decribes the structures of giant covalent substances like diamond, graphite and silicon dioxide (silicon(IV) oxide), and relates those structures to the physical properties of the substances. The structure of diamondThe giant covalent structure of diamond Carbon has an electronic arrangement of 2,4. In diamond, each carbon shares electrons with four other carbon atoms - forming four single bonds.
In the diagram some carbon atoms only seem to be forming two bonds (or even one bond), but that's not really the case. We are only showing a small bit of the whole structure. This is a giant covalent structure - it continues on and on in three dimensions. It is not a molecule, because the number of atoms joined up in a real diamond is completely variable - depending on the size of the crystal. |
|
|
Note: We quoted the electronic structure of carbon as 2,4. That simple view is perfectly adequate to explain the bonding in diamond. If you are interested in a more modern view, you could read the page on bonding in methane and ethane in the organic section of this site. In the case of diamond, each carbon is bonded to 4 other carbons rather than hydrogens, but that makes no essential difference. |
|
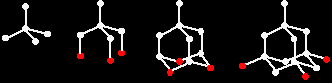
How to draw the structure of diamond Don't try to be too clever by trying to draw too much of the structure! Learn to draw the diagram given above. Do it in the following stages:
Practise until you can do a reasonable free-hand sketch in about 30 seconds. The physical properties of diamond Diamond
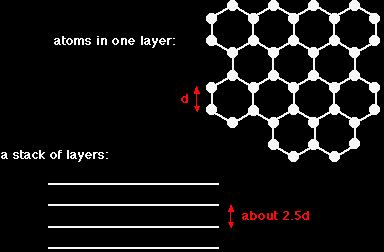
The structure of graphiteThe giant covalent structure of graphite Graphite has a layer structure which is quite difficult to draw convincingly in three dimensions. The diagram below shows the arrangement of the atoms in each layer, and the way the layers are spaced.
Notice that you can't really draw the side view of the layers to the same scale as the atoms in the layer without one or other part of the diagram being either very spread out or very squashed. In that case, it is important to give some idea of the distances involved. The distance between the layers is about 2.5 times the distance between the atoms within each layer. The layers, of course, extend over huge numbers of atoms - not just the few shown above. You might argue that carbon has to form 4 bonds because of its 4 unpaired electrons, whereas in this diagram it only seems to be forming 3 bonds to the neighbouring carbons. This diagram is something of a simplification, and shows the arrangement of atoms rather than the bonding. The bonding in graphite Each carbon atom uses three of its electrons to form simple bonds to its three close neighbours. That leaves a fourth electron in the bonding level. These "spare" electrons in each carbon atom become delocalised over the whole of the sheet of atoms in one layer. They are no longer associated directly with any particular atom or pair of atoms, but are free to wander throughout the whole sheet. |
|
|
If you are interested (beyond A'level): The bonding in graphite is like a vastly extended version of the bonding in benzene. Each carbon atom undergoes sp2 hybridisation, and then the unhybridised p orbitals on each carbon atom overlap sideways to give a massive pi system above and below the plane of the sheet of atoms. |
|
The important thing is that the delocalised electrons are free to move anywhere within the sheet - each electron is no longer fixed to a particular carbon atom. There is, however, no direct contact between the delocalised electrons in one sheet and those in the neighbouring sheets. The atoms within a sheet are held together by strong covalent bonds - stronger, in fact, than in diamond because of the additional bonding caused by the delocalised electrons. So what holds the sheets together? In graphite you have the ultimate example of van der Waals dispersion forces. As the delocalised electrons move around in the sheet, very large temporary dipoles can be set up which will induce opposite dipoles in the sheets above and below - and so on throughout the whole graphite crystal. |
|
|
Note: If you aren't sure about van der Waals forces follow this link before you go on. Use the BACK button on your browser to return to this page. |
|
The physical properties of graphite Graphite
|
|
|
Note: The logic of this is that a piece of graphite ought only to conduct electricity in 2-dimensions because electrons can only move around in the sheets - and not from one sheet to its neighbours. In practice, a real piece of graphite isn't a perfect crystal, but a host of small crystals stuck together at all sorts of angles. Electrons will be able to find a route through the large piece of graphite in all directions by moving from one small crystal to the next. |
|
The structure of silicon dioxide, SiO2Silicon dioxide is also known as silicon(IV) oxide. The giant covalent structure of silicon dioxide There are three different crystal forms of silicon dioxide. The easiest one to remember and draw is based on the diamond structure. Crystalline silicon has the same structure as diamond. To turn it into silicon dioxide, all you need to do is to modify the silicon structure by including some oxygen atoms.
Notice that each silicon atom is bridged to its neighbours by an oxygen atom. Don't forget that this is just a tiny part of a giant structure extending on all 3 dimensions. |
|
|
Note: If you want to be fussy, the Si-O-Si bond angles are wrong in this diagram. In reality the "bridge" from one silicon atom to its neighbour isn't in a straight line, but via a "V" shape (similar to the shape around the oxygen atom in a water molecule). It's extremely difficult to draw that convincingly and tidily in a diagram involving this number of atoms. The simplification is perfectly acceptable. |
|
The physical properties of silicon dioxide Silicon dioxide
|
|