Superposition
Principle of Superposition: When two or more waves of the same type meet at a point, the resultant displacement of the waves is equal to the vector sum of their individual displacements at that point.
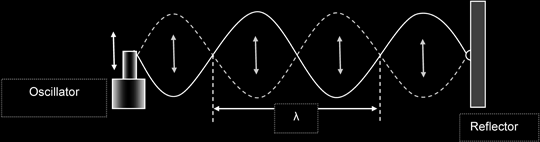
Stretched String
A horizontal rope with one end fixed and another attached to a vertical oscillator. Stationary waves will be produced by the direct and reflected waves in the string.
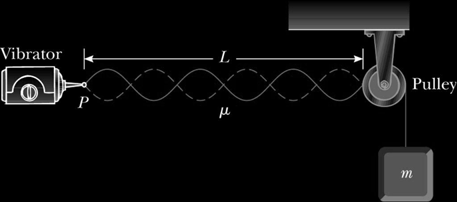
Or we can have the string stopped at one end with a pulley as shown below.
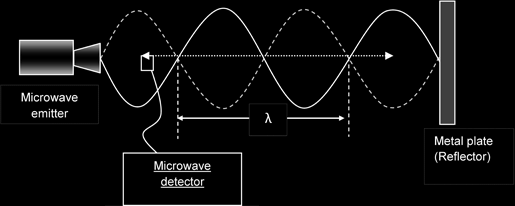
Microwaves
A microwave emitter placed a distance away from a metal plate that reflects the emitted wave. By moving a detector along the path of the wave, the nodes and antinodes could be detected.
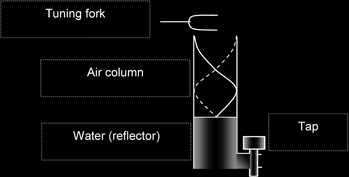
Air column
A tuning fork held at the mouth of a open tube projects a sound wave into the column of air in the tube. The length of the tube can be changed by varying the water level. At certain lengths of the tube, the air column resonates with the tuning fork. This is due to the formation of stationary waves by the incident and reflected sound waves at the water surface.
Stationary (Standing) Wave) is one
- whose waveform/wave profile does not advance {move},
- where there is no net transport of energy, and
- where the positions of antinodes and nodes do not change (with time).
A stationary wave is formed when two progressive waves of the same frequency, amplitude and speed, travelling in opposite directions are superposed. {Assume boundary conditions are met}
| Stationary Waves | Stationary Waves Progressive Waves | |
|---|---|---|
| Amplitude | Varies from maximum at the anti-nodes to zero at the nodes. | Same for all particles in the wave (provided no energy is lost). |
| Wavelength | Twice the distance between a pair of adjacent nodes or anti-nodes. | The distance between two consecutive points on a wave, that are in phase. |
| Phase | Particles in the same segment/ between 2 adjacent nodes, are in phase. Particles in adjacent segments are in anti-phase. | All particles within one wavelength have different phases. |
| Wave Profile | The wave profile does not advance. | The wave profile advances. |
| Energy | No energy is transported by the wave. | Energy is transported in the direction of the wave. |
Node is a region of destructive superposition where the waves always meet out of phase by π radians. Hence displacement here is permanently zero {or minimum}.
Antinode is a region of constructive superposition where the waves always meet in phase. Hence a particle here vibrates with maximum amplitude {but it is NOT a pt with a permanent large displacement!}
Dist between 2 successive nodes / antinodes = λ / 2
Max pressure change occurs at the nodes {NOT the antinodes} because every node changes fr being a pt of compression to become a pt of rarefaction {half a period later}
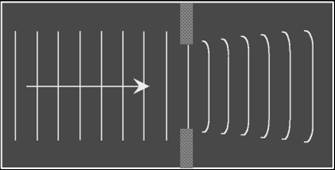
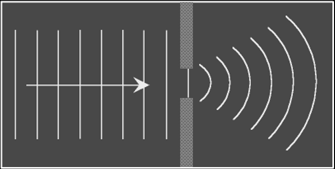
Diffraction: refers to the spreading {or bending} of waves when they pass through an opening {gap}, or round an obstacle (into the “shadow” region). {Illustrate with diag}
For significant diffraction to occur, the size of the gap ≈ λ of the wave
For a diffraction grating, d sin θ = n λ ,
d = dist between successive slits {grating spacing} = reciprocal of number of lines per metre
When a “white light” passes through a diffraction grating, for each order of diffraction, a longer wavelength {red} diffracts more than a shorter wavelength {violet} {as sin θ ∝ λ}.
Diffraction refers to the spreading of waves as they pass through a narrow slit or near an obstacle.
For diffraction to occur, the size of the gap should approximately be equal to the wavelength of the wave.
Coherent waves: Waves having a constant phase difference {not: zero phase difference / in phase}
Interference may be described as the superposition of waves from 2 coherent sources.
For an observable / well-defined interference pattern, the waves must be coherent, have about the same amplitude, be unpolarised or polarised in the same direction, & be of the same type.
Two-source interference using:
1. Water Waves
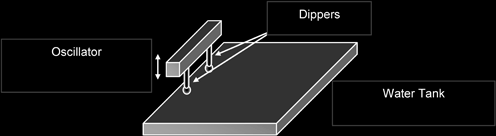
Interference patterns could be observed when two dippers are attached to the vibrator of the ripple tank. The ripples produce constructive and destructive interference. The dippers are coherent sources because they are fixed to the same vibrator.
2. Microwaves
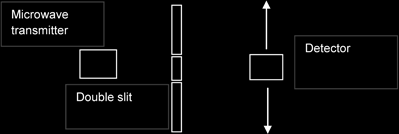
Microwave emitted from a transmitter through 2 slits on a metal plate would also produce interference patterns. By moving a detector on the opposite side of the metal plate, a series of rise and fall in amplitude of the wave would be registered.
3. Light Waves (Young‟s double slit experiment)
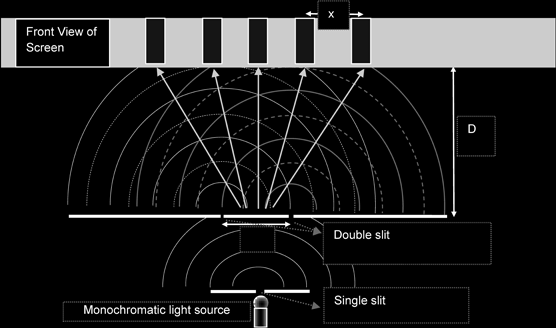
Since light is emitted from a bulb randomly, the way to obtain two coherent light sources is by splitting light from a single slit.
The 2 beams from the double slit would then interfere with each other, creating a pattern of alternate bright and dark fringes (or high and low intensities) at regular intervals, which is also known as our interference pattern.

Condition for Constructive Interference at a pt P:
Phase difference of the 2 waves at P = 0 {or 2π, 4π, etc}
Thus, with 2 in-phase sources, * implies path difference = nλ; with 2 antiphase sources: path difference = (n + ½)λ
Condition for Destructive Interference at a pt P:
Phase difference of the 2 waves at P = π { or 3π, 5π, etc }
With 2 in-phase sources, + implies path difference = (n+ ½ λ), with 2 antiphase sources: path difference = n λ
Fringe separation x = λD / a,
if a<<D {applies only to Young's Double Slit interference of light, ie, NOT for microwaves, sound waves, water waves}
Phase difference Δφ betw the 2 waves at any pt X {betw the central & 1st maxima) is (approx) proportional to the dist of X from the central maxima.
Using 2 sources of equal amplitude x0, the resultant amplitude of a bright fringe would be doubled {2x0}, & the resultant intensity increases by 4 times {not 2 times}. { IResultant ∝ (2 x0)2 }