Measurement

Base quantities and their units; mass (kg), length (m), time (s), current (A), temperature (K), amount of substance (mol):

Base Quantities	SI Units
	Name	Symbol
Length	metre	m
Mass	kilogram	kg
Time	second	s
Amount of substance	mole	mol
Temperature	Kelvin	K
Current	ampere	A
Luminous intensity	candela	cd

Derived units as products or quotients of the base units:

Derived	Quantities Equation	Derived Units
Area (A)	A = L2	m2
Volume (V)	V = L3	m3
Density (ρ)	ρ = m / V	kg m-3
Velocity (v)	v = L / t	ms-1
Acceleration (a)	a = Δv / t	ms-1 / s = ms-2
Momentum (p)	p = m x v	(kg)(ms-1) = kg m s-1

Derived Quantities	Equation	Derived Unit		Derived Units
		Special Name	Symbol
Force (F)	F = Δp / t	Newton	N	[(kg m s-1) / s = kg m s-2
Pressure (p)	p = F / A	Pascal	Pa	(kg m s-2) / m2 = kg m-1 s-2
Energy (E)	E = F x d	joule	J	(kg m s-2)(m) = kg m2 s-2
Power (P)	P = E / t	watt	W	(kg m2 s-2) / s = kg m2 s-3
Frequency (f)	f = 1 / t	hertz	Hz	1 / s = s-1
Charge (Q)	Q = I x t	coulomb	C	A s
Potential Difference (V)	V = E / Q	volt	V	(kg m2 s-2) / A s = kg m2 s-3 A-1
Resistance (R)	R = V / I	ohm	Ω	(kg m2 s-3 A-1) / A = kg m2 s-3 A-2

Prefixes and their symbols to indicate decimal sub-multiples or multiples of both base and derived units:

Multiplying Factor	Prefix	Symbol
10-12	pico	p
10-9	nano	n
10-6	micro	μ
10-3	milli	m
10-2	centi	c
10-1	decid	d
103	kilo	k
106	mega	M
109	giga	G
1012	tera	T

 

Estimates of physical quantities:

When making an estimate, it is only reasonable to give the figure to 1 or at most 2 significant figures since an estimate is not very precise.

Physical Quantity	Reasonable Estimate
Mass of 3 cans (330 ml) of Coke	1 kg
Mass of a medium-sized car	1000 kg
Length of a football field	100 m
Reaction time of a young man	0.2 s

• Occasionally, students are asked to estimate the area under a graph. The usual method of counting squares within the enclosed area is used. (eg. Topic 3 (Dynamics), N94P2Q1c)
• Often, when making an estimate, a formula and a simple calculation may be involved.

EXAMPLE 1:

Estimate the average running speed of a typical 17-year-old‟s 2.4-km run.

velocity = distance / time = 2400 / (12.5 x 60) = 3.2 ≈3 ms^-1

EXAMPLE 2:

Which estimate is realistic?

	Option	Explanation
A	The kinetic energy of a bus travelling on an expressway is 30000J	A bus of mass m travelling on an expressway will travel between 50 to 80 kmh-1, which is 13.8 to 22.2 ms-1. Thus, its KE will be approximately ½ m(182) = 162m. Thus, for its KE to be 30000J: 162m = 30000. Thus, m = 185kg, which is an absurd weight for a bus; ie. This is not a realistic estimate.
B	The power of a domestic light is 300W.	A single light bulb in the house usually runs at about 20W to 60W. Thus, a domestic light is unlikely to run at more than 200W; this estimate is rather high.
C	The temperature of a hot oven is 300 K.	300K = 27 0C. Not very hot.
D	The volume of air in a car tyre is 0.03 m3.		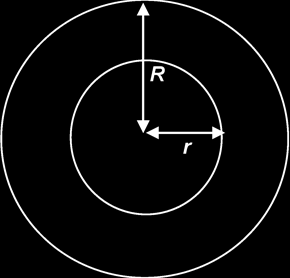Estimating the width of a tyre, t, is 15 cm or 0.15 m, and estimating R to be 40 cm and r to be 30 cm, volume of air in a car tyre is = π(R2 – r2)t = π(0.42 – 0.32)(0.15) = 0.033 m3 ≈ 0.03 m3 (to one sig. fig.)

 

Distinction between systematic errors (including zero errors) and random errors and between precision and accuracy:

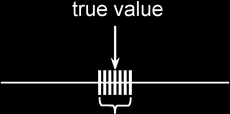
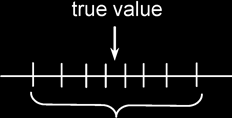
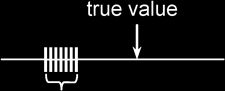
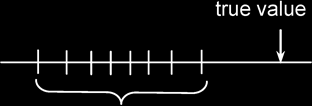
Random error: is the type of error which causes readings to scatter about the true value.

Systematic error: is the type of error which causes readings to deviate in one direction from the true value.

Precision: refers to the degree of agreement (scatter, spread) of repeated measurements of the same quantity. {NB: regardless of whether or not they are correct.}

Accuracy: refers to the degree of agreement between the result of a measurement and the true value of the quantity.

	→ → R Error Higher → → → → → → Less Precise → → →
↓ ↓ ↓ S Error Higher Less Accurate ↓ ↓ ↓

Assess the uncertainty in a derived quantity by simple addition of actual, fractional or percentage uncertainties (a rigorous statistical treatment is not required).

For a quantity x = (2.0 ± 0.1) mm,

Actual/ Absolute uncertainty, Δ x = ± 0.1 mm

Fractional uncertainty, Δxx = 0.05

Percentage uncertainty, Δxx  100% = 5 %

If p = (2x + y) / 3 or p = (2x - y) / 3 , Δp = (2Δx + Δy) / 3

If r = 2xy³ or r = 2x / y³ , Δr / r = Δx / x + 3Δy / y

Actual error must be recorded to only 1 significant figure, &
The number of decimal places a calculated quantity should have is determined by its actual error.

For eg, suppose g has been initially calculated to be 9.80645 ms^-2 & Δg has been initially calculated to be 0.04848 ms^-2. The final value of Δg must be recorded as 0.05 ms^-2 {1 sf }, and the appropriate recording of g is (9.81 ± 0.05) ms^-2.

Distinction between scalar and vector quantities:

	Scalar	Vector
Definition	A scalar quantity has a magnitude only. It is completely described by a certain number and a unit.	A vector quantity has both magnitude and direction. It can be described by an arrow whose length represents the magnitude of the vector and the arrow-head represents the direction of the vector.
Examples	Distance, speed, mass, time, temperature, work done, kinetic energy, pressure, power, electric charge etc. Common Error: Students tend to associate kinetic energy and pressure with vectors because of the vector components involved. However, such considerations have no bearings on whether the quantity is a vector or scalar.	Displacement, velocity, moments (or torque), momentum, force, electric field etc.

Representation of vector as two perpendicular components:

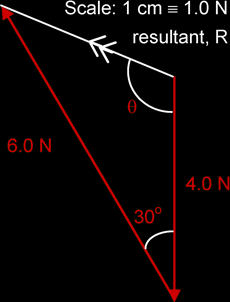
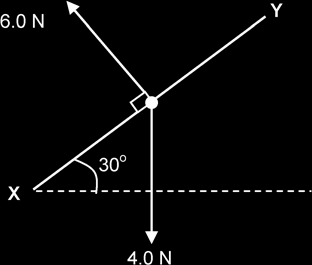
In the diagram below, XY represents a flat kite of weight 4.0 N. At a certain instant, XY is inclined at 30° to the horizontal and the wind exerts a steady force of 6.0 N at right angles to XY so that the kite flies freely.

By accurate scale drawing	By calculations using sine and cosine rules, or Pythagoras‟ theorem
Draw a scale diagram to find the magnitude and direction of the resultant force acting on the kite. R = 3.2 N (≡ 3.2 cm) at θ = 112° to the 4 N vector.	Using cosine rule, a2 = b2 + c2 – 2bc cos A R2 = 42 + 62 -2(4)(6)(cos 30°) R = 3.23 N Using sine rule: a / sin A = b / sin B 6 / sin α = 3.23 / sin 30° α = 68° or 112° = 112° to the 4 N vector

 

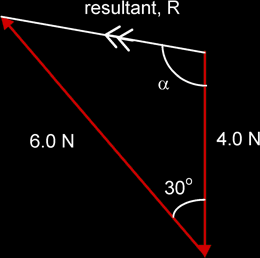
Summing Vector Components
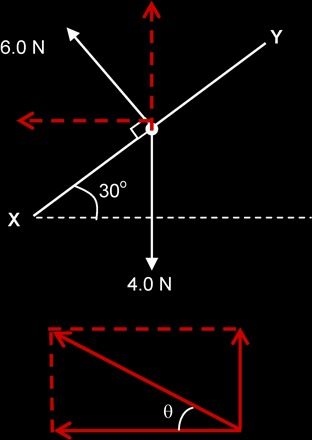	Fx = - 6 sin 30° = - 3 N Fy = 6 cos 30° - 4 = 1.2 N R = √(-32 + 1.22) = 3.23 N tan θ = 1.2 / 3 = 22° R is at an angle 112° to the 4 N vector. (90° + 22°)

This temporary old revision section will automatically redirect to new version once ready.