Electric Fields
Electric field strength / intensity at a point is defined as the force per unit positive charge acting at that point {a vector; Unit: N C-1 or V m-1}
E = F / q → F = qE
- The electric force on a positive charge in an electric field is in the direction of E, while
- The electric force on a negative charge is opposite to the direction of E.
- Hence a +ve charge placed in an electric field will accelerate in the direction of E and gain KE {& simultaneously lose EPE}, while a negative charge caused to move (projected) in the direction of E will decelerate, ie lose KE, { & gain EPE}.
Representation of electric fields by field lines
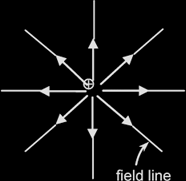 |
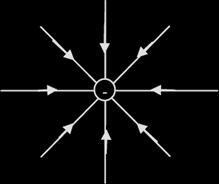 |
 |
 |
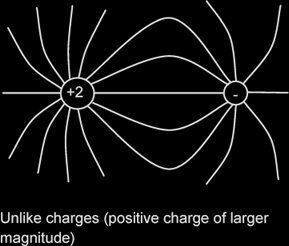 |
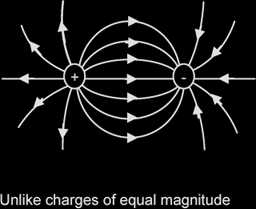 |
Coulomb's law:
The (mutual) electric force F acting between 2 point charges Q1 and Q2 separated by a distance r is given by:
F = Q1Q2 / 4πεor2 where ε0: permittivity of free space
or, the (mutual) electric force between two point charges is proportional to the product of their charges & inversely proportional to the square of their separation.
Example 1:
Two positive charges, each 4.18 μC, and a negative charge, -6.36 μC, are fixed at the vertices of an equilateral triangle of side 13.0 cm. Find the electrostatic force on the negative charge.
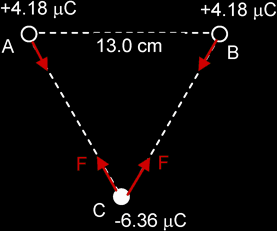 |
F = Q1Q2 / 4πεor2
(Note: negative sign for -6.36 μC has been ignored in the calculation) FR = 2 x Fcos300
|
Electric field strength due to a Point Charge Q : E = Q / 4πεor2
{NB: Do NOT substitute a negative Q with its negative sign in calculations!}
Example 2:
In the figure below, determine the point (other than at infinity) at which the total electric field strength is zero.

From the diagram, it can be observed that the point where E is zero lies on a straight line where the charges lie, to the left of
the -2.5 μC charge.
Let this point be a distance r from the left charge.
Since the total electric field strength is zero,
E6μ = E-2μ
[6μ / (1 + r)2] / 4πεor2 = [2.5μ / r2] / 4πεor2 (Note: negative sign for -2.5 μC has been ignored here)
6 / (1 + r)2 = 2.5 / r2
√(6r) = 2.5 (1 + r)
r = 1.82 m
The point lies on a straight line where the charges lie, 1.82 m to the left of the -2.5 μC charge.
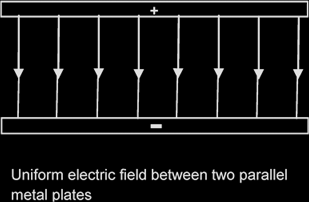
Uniform electric field between 2 Charged Parallel Plates: E = Vd,
d: perpendicular dist between the plates,
V: potential difference between plates
Path of charge moving at 90° to electric field: parabolic.
Beyond the pt where it exits the field, the path is a straight line, at a tangent to the parabola at exit.
Example 3:
An electron (m = 9.11 x 10-31 kg; q = -1.6 x 10-19 C) moving with a speed of 1.5 x 107 ms-1, enters a region between 2 parallel plates, which are 20 mm apart and 60 mm long. The top plate is at a potential of 80 V relative to the lower plate. Determine the angle through which the electron has been deflected as a result of passing through the plates.
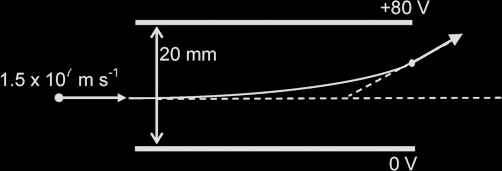
Time taken for the electron to travel 60 mm horizontally = Distance / Speed = 60 x 10-3 / 1.5 x 107 = 4 x 10-9 s
E = V / d = 80 / 20 x 10-3 = 4000 V m-1
a = F / m = eE / m = (1.6 x 10-19)(4000) / (9.1 x 10-31) = 7.0 x 1014 ms-2
vy = uy + at = 0 + (7.0 x 1014)( 4 x 10-9) = 2.8 x 106 ms-1
tan θ = vy / vx = 2.8 x 106 / 1.5 x 107 = 0.187
Therefore θ = 10.6°
Effect of a uniform electric field on the motion of charged particles
- Equipotential surface: a surface where the electric potential is constant
- Potential gradient = 0, ie E along surface = 0 }
- Hence no work is done when a charge is moved along this surface.{ W=QV, V=0 }
- Electric field lines must meet this surface at right angles.
- {If the field lines are not at 90° to it, it would imply that there is a non-zero component of E along the surface. This would contradict the fact that E along an equipotential = 0. }
Electric potential at a point: is defined as the work done in moving a unit positive charge from infinity to that point, { a scalar; unit: V } ie V = W / Q
The electric potential at infinity is defined as zero. At any other point, it may be positive or negative depending on the sign of Q that sets up the field. {Contrast gravitational potential.}
Relation between E and V: E = - dV / dr
i.e. The electric field strength at a pt is numerically equal to the potential gradient at that pt.
NB: Electric field lines point in direction of decreasing potential {ie from high to low pot}.
Electric potential energy U of a charge Q at a pt where the potential is V: U = QV
Work done W on a charge Q in moving it across a pd ΔV: W = Q ΔV
Electric Potential due to a point charge Q : V = Q / 4πεor
{NB: Substitute Q with its sign}